
MATLAB is develop for mathematics, therefore MATLAB is the abbreviation of MATrix LABoratory.Īt here, we find the root of the function f(x) = x 2-2 = 0 by using Bisection method with the help of MATLAB. MATLAB is easy way to solve complicated problems that are not solve by hand or impossible to solve at page. It is also called Interval halving, binary search method and. It is a very simple and robust method but slower than other methods. Bisection Method repeatedly bisects an interval and then selects a subinterval in which root lies.
#Bisection method root finding code
The disadvantage of this method is that it is slow compare than other numerical methods to solve nonlinear equation.Īt here, we write the code of Bisection Method in MATLAB step by step. Bisection method algorithm is very easy to program and it always converges which means it always finds root. Bisection method is bracketing method because its roots lie within the interval.

It is also known as binary search method, interval halving method, the binary search method, or the dichotomy method and Bolzano’s method. Because of this, it is often used to obtain a rough approximation to a solution which is then used as a starting point for more rapidly converging. When an equation has multiple roots, it is the choice of the initial interval provided by the user which determines which root is located. It is a very simple and robust method, but it is also relatively slow. The Bisection method fails to identify multiple different roots, which makes it less desirable to use compared to other methods that can identify multiple roots. Here we discuss an introduction to Bisection Method Matlab, syntax, parameters, and examples for better understanding.Bisection method is root finding method of non-linear equation in numerical method. The bisection method in mathematics is a root-finding method that repeatedly bisects an interval and then selects a sub-interval in which a root must lie for further processing. This is a guide to Bisection Method Matlab. As there is no direct function for the bisection rule in MATLAB, we define the code or logic for it manually. For a given function f (x) ,the Bisection Method algorithm works as follows: two values a and b are chosen for which f (a) > 0 and f (b) < 0 (or the other way around) interval halving: a midpoint c is calculated as the arithmetic mean between a and b, c (a + b) / 2 the function f is evaluated for. The bisection method is used to find the root of any polynomial function. For this example, we will input the following values:Īs we can see in the output, we have obtained the root of our input function as 1.7344, after we input our guess values for the first time. Bisection method text notesPPT is one of the first numerical methods developed to find the root of a nonlinear equation f(x)0 (also. We will use the code above and will pass the inputs as asked. In this example, we will take a polynomial function of degree 2 and will find its roots using the bisection method. Next, let us see an example where we are not asked for the guess values the second time Example #3 The code will again ask for firstValue and endValueĪs we can see in the output, we have obtained the root of our input function as 2.5.The result is the search technique known as bisection or Bolzano's method. Pass the input function as 3*x.^3 + 2*x.^2 f to one of finding the root of a monotone function g on the same interval.For this example, we will input the following values: In this example, we will take a polynomial function of degree 3 and will find its roots using the bisection method. Pass the firstValue as 2 and endValue as 3 this timeĪs we can see in the output, we have obtained the root of our input function as 2.5.If the root does not lie between 1 & 2, then the code will again ask for firstValue and endValue.For our first example, we will input the following values:
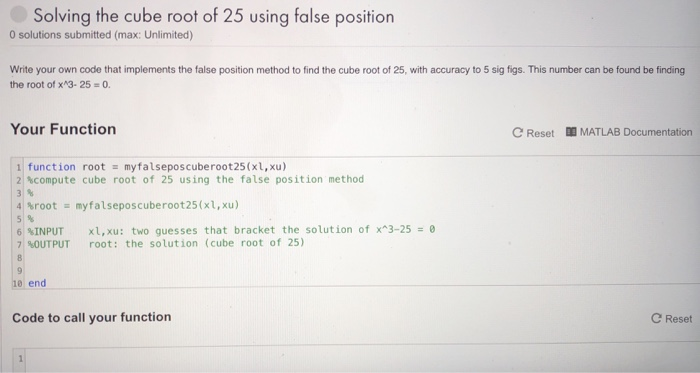
A root of the equation f (x) 0 is also called a.

If the function equals zero, x is the root of the function. For a given function f (x), the process of finding the root involves finding the value of x for which f (x) 0.


 0 kommentar(er)
0 kommentar(er)
